最近一直在忙着考试，就没有时间学习Java，后天也就是下周一还有最后一科考试“系统建模与仿真”–比较水的一门课，所以也就腾出来了一点时间，就想总结一下研究生第一学期学习的课程。

1. 英语

研究生还要学习英语，一开始觉得真是让人头疼，后来觉得还是蛮实用的。英语分为了听说、读写，听说主要学习了一些演讲、申请留学和工作面试的表达；读写主要学习中西方语言表达的差异，这部分讲的很细致，对以后论文的写作很有帮助，可惜上课听得较少，大部分还是通过考试前自学的。

2. 矩阵论

矩阵论就是大学线性代数的延伸，一开始学习这门课最令我震惊的是即使是一个函数表达式也可以写成矩阵的形式，并且可以进行相关的运算。随着课程的深入，也让我意识到这门课的重要性，尤其是对于数字图像处理领域，几乎是离不开矩阵论的思想。
这门课还需要写一篇课程论文，我写的是“基于SVD的图像压缩算法实现”，利用奇异值分解的性质，对图像进行压缩，因为奇异值分解可以降低矩阵的维度，奇异值较小的，所含的能量也较低，将这些奇异值和对应的向量消除，从而减少存储空间。
主要内容为：

1) 线性空间与线性变换

2) 内积空间与等距变换

3) 矩阵的Jordan标准型

4) 矩阵分解

5) 矩阵分析

6) 矩阵的广义逆

3. 随机过程

相应的随机过程也就是大学概率论的延伸，这里不再仅仅局限在一个或者几个随机变量，而是在每一个时刻都是一个随机变量，将这些时刻串在一起就构成了随机过程。这门课后面部分平稳过程的谱分析，谱密度还是挺让人头大的（想想大学的傅里叶变换就知道啦，哈哈！），即使今天考完啦，做出来啦，但还是不太懂得其中的意思。或许以后工程上用到的时候会有一个较深的理解吧。
主要内容为：

1) 泊松过程

2) 离散马尔科夫链

3) 连续马尔科夫链

4) 平稳过程

4. 系统建模与仿真

这门虽然有点“水”，但是用处很大，主要是讲线性系统的仿真，人工神经网络，BP神经网络，模拟退火算法，遗传算法。，每一部分拉出来都是可以讲一个学期的，然而我们17周，一周两节课就结束啦，或许这就是考验研究生自学能力的时候吧！
主要内容：

1) 线性时不变系统的数学模型及其仿真
这一部分的内容和大学信号与系统的内容一样，这里就是大概的过一遍大学所学的知识点，涉及到拉式变换、传递函数、状态方程的求解、系统的各种数学模型之间的相互转换、系统模型的连接以及系统的离散化和连续化。

2) 随机数的产生与混沌
讲了两个重要的随机数产生方法

乘同余法xi+1=A xi mod(M) 根据数论的理论证明：计算机位数为L，如果模数M=2L, 当

（1）A=8k±3， A=4k+1，k为正整数；
（2）x0为奇数时，可以获得最长的随机序列长度为2L-2。

混合同余法，也称线性同余xi+1=(A xi +B)mod(M) 根据数论的理论证明：计算机位数为L，如果模数M=2L, 当

（1）A=4k+1，k为正整数；
（2）B与M互为质数时，可以获得最长的随机序列长度为2L。
3) 神经网络
这里只是一个入门，只是讲解了人工神经网络的基本概念、单层网、多层网、循环网等各种基本网络模型的结构、特点、典型训练算法、运行方式、典型问题。
这部分值得思考的几点问题：

为什么需要激活函数？
不同激活函数之间的优缺点或者说具体的应用？
为什么需要偏置？
这里还是推荐斯坦福大学吴恩达博士的机器学习课程
讲解的很细致。
4) 遗传算法
这个对我来说还是比较熟悉的，因为本科毕设使用到了基因表达式编程算法就和这个算法有些类似。区别可以用下图展示：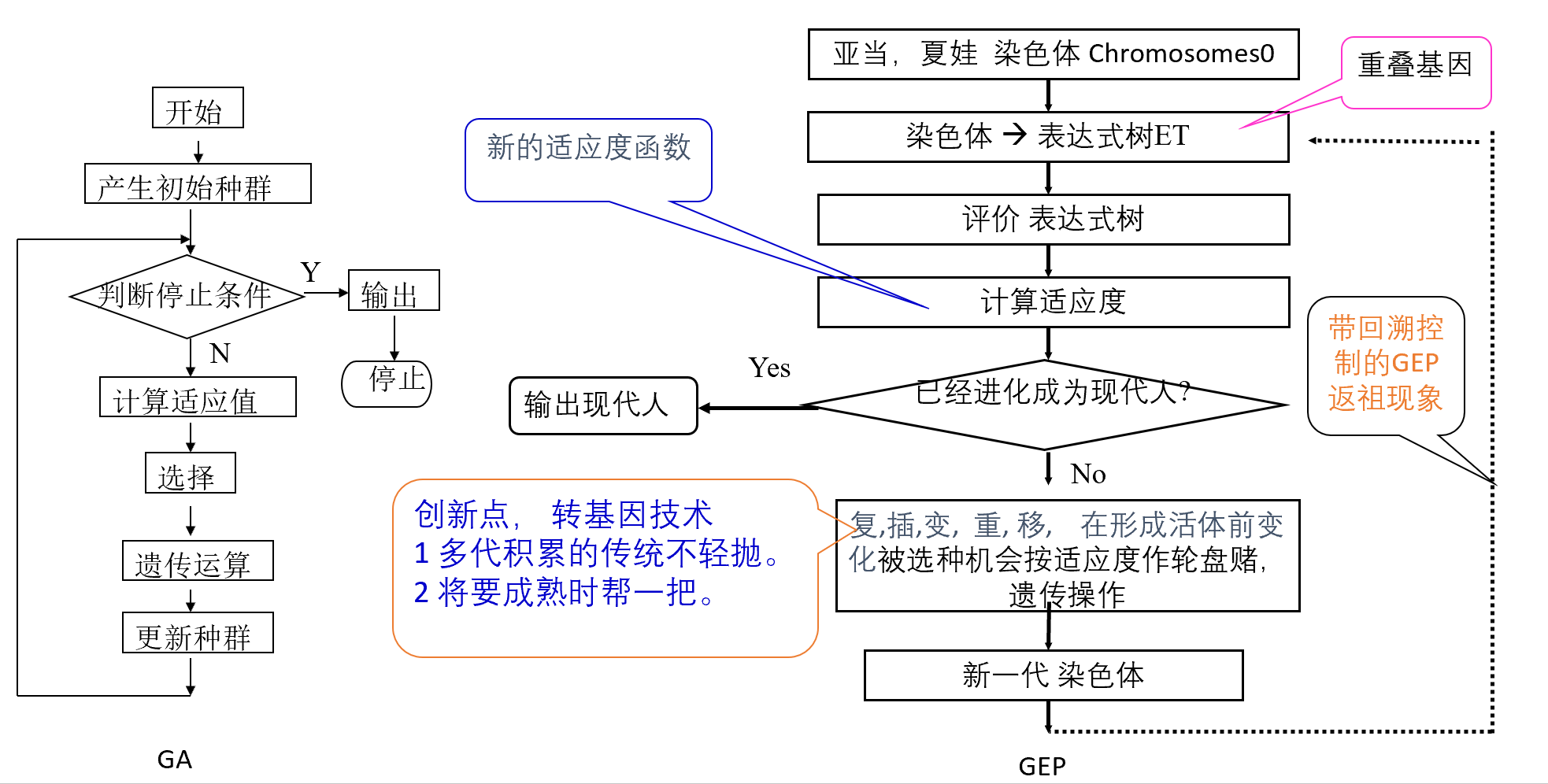

5) 模拟退火算法
模拟退火算法包括三函数两准则，即状态产生函数、状态接受函数、温度更新函数、内循环终止准则和外循环终止准则，这些环节的设计将决定SA算法的优化性能。此外，初温的选择对SA算法性能也有很大影响。还需要注意：降温过快， SA很快从广域搜索转为局域搜索，很可能过早陷于局部最优。
降温过慢，外循环次数增大，浪费时间。