栈 | Qu-jq’s Blog

生活中经常会使用到计算器，要计算”1+2*3-1“时，就需要用到栈这个数据结构

1. 定义

1) 栈的英文为(stack)

2) 栈是一个先入后出(FILO-First In Last Out)的有序列表。

3) 栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端，为变化的一端，称为栈顶(Top)，另一端为固定的一端，称为栈底(Bottom)。

4) 根据栈的定义可知，最先放入栈中元素在栈底，最后放入的元素在栈顶，而删除元素刚好相反，最后放入的元素最先删除，最先放入的元素最后删除

2. 应用场景

1) 子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以回到原来的程序中。

2) 处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外，也将参数、区域变量等数据存入堆栈中。

3) 表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。

4) 二叉树的遍历。

5) 图形的深度优先(depth一first)搜索法。

3.数组模拟栈

1) 思路分析

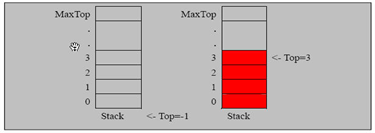
使用数组来模拟栈
定义一个 top 来表示栈顶，初始化为 -1
入栈的操作，当有数据加入到栈时， top++; stack[top] = data;
出栈的操作， int value = stack[top]; top–, return value

栈数组

2）Java程序实现

package datastructure;

import java.util.Scanner;

/**
 * 使用数组模拟栈
 * Created by qjq on 2020/1/28 16:29
 */
public class ArrayStackDemo {
    //测试
    public static void main(String[] args) {
        ArrayStack arrayStack = new ArrayStack(4);
        String mark;
        Scanner scanner = new Scanner(System.in);//键盘输入
        boolean flag = true;//循环标志位
        while(flag){
            System.out.println("show:显示栈");
            System.out.println("pop:出栈");
            System.out.println("push:入栈");
            System.out.println("exit:退出");
            System.out.println("请输入你的选择：");
            mark = scanner.next();
            switch (mark){
                case "show":
                    arrayStack.list();
                    break;
                case "pop":
                    try {
                        int res = arrayStack.pop();
                        System.out.println("出栈的数据是："+res);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }
                    break;
                case "push":
                    System.out.println("请输入入栈数据：");
                    int val = scanner.nextInt();
                    arrayStack.push(val);
                    break;
                case "exit":
                    flag=false;
                    break;
            }
        }
    }
}

/**
 * 创建模拟栈的类
 */
class ArrayStack{
    private int maxSize;
    private int[] stack;
    private int top;//模拟栈顶指针

    /**
     * 构造器
     * @param maxSize 数组的最大容量
     */
    public ArrayStack(int maxSize) {
        this.maxSize = maxSize;
        stack = new int[maxSize];
        top=-1;//初始值默认为-1
    }

    /**
     * 判断栈是否满
     * @return 真假
     */
    public boolean isFull(){
        return top == maxSize-1;
    }

    /**
     * 入栈
     * @param data 入栈数据
     */
    public void push(int data){
        if (isFull()){
            System.out.println("栈已满，无法入栈");
            return;
        }
        top++;
        stack[top] = data;
    }

    /**
     * 出栈
     * @return 返回出栈数据
     */
    public int pop(){
        if (top == -1){
            throw new RuntimeException("栈为空");
        }
        int value = stack[top];
        top--;
        return value;
    }

    /**
     * 遍历栈 从顶部开始
     */
    public void list(){
        if(top == -1){
            System.out.println("栈为空");
        }
        for (int i = top; i >= 0 ; i--) {
            System.out.printf("stack[%d]=%d\n",i,stack[i]);
        }
    }
}

4. 链表模拟栈

1）思路分析

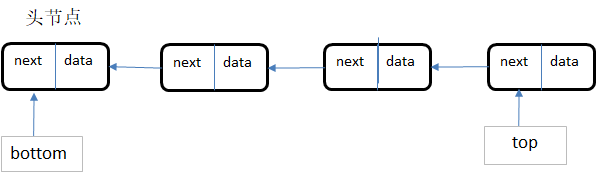
首先需要定义链表节点：数据域+指针域
栈的结构为：栈顶top+栈底bottom
栈底为空，保持不动，栈顶进行入栈、出栈的操作
目的是便于出栈入栈：注意此处链表的方向和以前的反过来，如下图所示。
出栈：value = top; top = top.next; return value;
入栈：newNode.next = top; top = newNode;

2）Java程序实现

package datastructure;

import java.util.Scanner;

/**
 * 使用链表模拟栈
 * 注意此处链表的方向和以前的反过来
 * [头节点1|next=null]<-[节点2|next]<-[节点3|next]
 * 目的是便于出栈入栈
 * Created by qjq on 2020/1/28 17:02
 */
public class LinkedListStackDemo {
    public static void main(String[] args) {
        LinkedListStack LLStack = new LinkedListStack();
        String mark;
        Scanner scanner = new Scanner(System.in);//键盘输入
        boolean flag = true;//循环标志位
        while(flag){
            System.out.println("show:显示栈");
            System.out.println("pop:出栈");
            System.out.println("push:入栈");
            System.out.println("exit:退出");
            System.out.println("请输入你的选择：");
            mark = scanner.next();
            switch (mark){
                case "show":
                    LLStack.list();
                    break;
                case "pop":
                    try {
                        LLNode res = LLStack.pop();
                        System.out.println("出栈的数据是："+res.data);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }
                    break;
                case "push":
                    System.out.println("请输入入栈数据：");
                    int val = scanner.nextInt();
                    LLStack.push(new LLNode(val));
                    break;
                case "exit":
                    flag=false;
                    break;
            }
        }
    }
}

/**
 * 链表节点
 */
class LLNode{
    Integer data;//数据域
    LLNode next;//指针域 默认为空

    public LLNode(Integer data) {
        this.data = data;
    }
}

class LinkedListStack{
    private LLNode top;//模拟栈顶指针
    private LLNode bottom;//模拟栈顶指针
    /**
     * 构造器：相当于初始化
     */
    public LinkedListStack() {
        bottom = new LLNode(null);//栈的头节点
        top= bottom;
    }

    /**
     * 入栈
     * @param llNode 入栈节点
     */
    public void push(LLNode llNode){
        llNode.next = top;//新节点的next指向顶部
        top = llNode;//top重新指向最顶端
    }

    /**
     * 出栈
     * @return 返回出栈数据
     */
    public LLNode pop(){
        if (top == bottom){
            throw new RuntimeException("栈为空");
        }
        LLNode temp;
        temp = top;
        top = top.next;//重新指向上一个节点
        return temp;
    }


    /**
     * 遍历栈 从顶部开始
     */
    public void list(){
        if(top == bottom){
            System.out.println("栈为空");
        }
        LLNode temp = top;
        while (temp!=bottom){
            System.out.print(temp.data + "\t");
            temp = temp.next;
        }
        System.out.println();
    }
}

3）C语言实现

#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>

typedef struct NODE {
	int data;//数据域
	struct NODE* pNEXT;//指针域
}NODE,*PNODE;

typedef struct STACK {
	PNODE pTOP; //栈顶
	PNODE pBottom;//栈底
}STACK,* pSTACK;

void Init_stack(pSTACK pS);
void push(pSTACK pS, int val);
void traverse(pSTACK pS);
bool pop(pSTACK pS,int *val);
void Clear_stack(pSTACK pS);
bool is_empty(pSTACK pS);
void main(void)
{
	STACK S;
	int val;
	Init_stack(&S);
	push(&S, 2);
	push(&S, 5);
	push(&S, 7);
	traverse(&S);
	push(&S, 2);
	push(&S, 5);
	push(&S, 7);
	traverse(&S);
	pop(&S, &val);
	printf("出栈的值为：%d\n", val);
	Clear_stack(&S);
	traverse(&S);
	return 0;
}

void Init_stack(pSTACK pS)
{
	PNODE P = (PNODE)malloc(sizeof(NODE));
	if (NULL == P)
	{
		printf("创建失败！");
		return;
	}
	P->pNEXT = NULL;
	pS->pTOP = P;
	pS->pBottom = pS->pTOP;
}

void push(pSTACK pS, int val)
{
	PNODE P = (PNODE)malloc(sizeof(NODE));//一定要注意是NODE  而不是PNODE
	if (NULL == P)
	{
		printf("创建失败！");
		return;
	}
	P->pNEXT = pS->pTOP;
	P->data = val;
	pS->pTOP = P;
}

bool is_empty(pSTACK pS)
{
	if (pS->pBottom == pS->pTOP)
	{
		return true;
	}
	else
		return false;
}
void traverse(pSTACK pS)
{
	PNODE pnew = pS->pTOP;//用来遍历栈
	if (is_empty(pS))
	{
		return;
	}
	else
	{
		while (pnew != pS->pBottom)//当不为空的时候
		{
			printf("%d\n", pnew->data);
			pnew = pnew->pNEXT;
		}	
	}
	//free(pnew);//此处不能释放地址，因为和pS->pBottom相同
	//pnew = NULL;
	return;
}

bool pop(pSTACK pS, int* val)
{
	if (is_empty(pS))
	{
		return false;
	}
	PNODE q = pS->pTOP;
	pS->pTOP = q->pNEXT;
	*val = q->data;
	free(q);//只是将内存归还操作系统 不会将指针置零
	q = NULL;
	return true;
}
void Clear_stack(pSTACK pS)
{
	//PNODE p = (PNODE)malloc(sizeof(NODE));
	PNODE p=pS->pTOP;
	PNODE q= pS->pTOP;
	if (q == NULL)
		return;
	if (p == NULL)
		return;
	while (p != pS->pBottom)
	{
		q = p->pNEXT;

		if (p != NULL)
		{
			free(p);
			p = NULL;
		}
		p = q;
		
	}
	pS->pTOP = pS->pBottom;
}

5.低级计算器应用

首先实现一个简单的计算器，如：5+4*2+8/2。不带括号。

1）思路分析

通过一个 index 值（索引），来遍历我们的表达式
如果我们发现是一个数字**,** 就直接入数栈
如果发现扫描到是一个符号, 就分如下情况

3.1 如果发现当前的符号栈为空，就直接入栈

3.2 如果符号栈有操作符，就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符，就需要从数栈中pop出两个数,在从符号栈中pop出一个符号，进行运算，将得到结果，入数栈，然后将当前的操作符再次与栈顶操作符比较（注意） ，如果当前的操作符的优先级大于栈中的操作符，就直接入符号栈
当表达式扫描完毕，就顺序的从数栈和符号栈中pop出相应的数和符号，并运行
最后在数栈只有一个数字，就是表达式的结果

2）Java程序实现

package datastructure;

import java.util.Scanner;

/**
 * 使用栈实现计算器功能
 * Created by qjq on 2020/1/30 10:02
 */
public class CalculateDemo {
    public static void main(String[] args) {
        Calculate<Character> operaStack = new Calculate<>();//存放运算符的栈
        Calculate<Integer> numStack = new Calculate<>();//存放数字的栈
        Scanner scanner = new Scanner(System.in);//键盘输入
        String calculateStr;//计算式子
        Character temp;//遍历计算式子
        boolean flag = true;//循环标志位
        boolean flag2 = true;//循环标志位
        System.out.println("请输入运算式：");
        calculateStr = scanner.next();
        System.out.println(calculateStr);
        //各个数据入栈
        //for (int i = 0; i < calculateStr.length(); i++) {
        int i =0;
        while (flag){
            temp = calculateStr.charAt(i);//读取计算式的第i个字符。
            //如果是数的话 直接入数栈
            if(!numStack.isOperation(temp)){
                //这里需要减去'0'，不然的话，转换的是为ASCII码
                numStack.push(new LLNode2<>((int) (temp-'0')));
            }else if(operaStack.isOperation(temp)){     //当为符号时
                //如果发现当前的符号栈为 空，就直接入栈
                if(operaStack.isEmpty()){
                    operaStack.push(new LLNode2<>(temp));
                    //此次循环结束，进行下一个符号
                    if (i == calculateStr.length() - 1) {
                        flag = false;
                    } else {
                        i++;
                    }
                    continue;
                }
                /*如果符号栈有操作符，就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符，
                 就需要从数栈中pop出两个数,在从符号栈中pop出一个符号，进行运算，将得到结果，入数栈，
                 然后将当前的操作符再次与栈顶操作符比较（注意）； 如果当前的操作符的优先级大于栈中的操作符， 就直接入符号栈.
                 */
                if(operaStack.isPrior(temp)<=operaStack.isPrior(operaStack.readLastData())){
                    Integer num1 = numStack.pop().data;
                    Integer num2 = numStack.pop().data;
                    Character opera = operaStack.pop().data;
                    Integer result = operaStack.calculate(num1,num2,opera);
                    numStack.push(new LLNode2<>(result));
                    continue;//此符号，再与下一个栈顶符号比较，因此这里不加入i++
                }else {
                    operaStack.push(new LLNode2<>(temp));
                }
            }
            //此符号结束，进行下一个符号
            if(i != (calculateStr.length() - 1)) {
                i++;
            } else {
                flag = false;
            }
        }
        numStack.list();
        operaStack.list();
        //出栈计算
        while(flag2){
            Integer num1 = numStack.pop().data;
            Integer num2 = numStack.pop().data;
            //当数据全部出栈完时，循环结束
            if (numStack.isEmpty()){
                flag2 = false;
            }
            Character opera = operaStack.pop().data;
            Integer result = operaStack.calculate(num1,num2,opera);
            //将最后结果压入栈中
            numStack.push(new LLNode2<>(result));
        }
        System.out.println("最后结果为："+numStack.readLastData());
    }
}

/**
 * 链表节点
 */
class LLNode2 <T>{
    T data;//数据域
    LLNode2<T> next;//指针域 默认为空

    public LLNode2(T data) {
        this.data = data;
    }
}

class Calculate<T> {
    private LLNode2<T> top;//模拟栈顶指针
    private LLNode2<T> bottom;//模拟栈顶指针
    /**
     * 构造器：相当于初始化
     */
    public Calculate() {
        bottom = new LLNode2<>(null);//栈的头节点
        top= bottom;
    }

    /**
     * 判断栈是否空
     * @return 真假
     */
    public boolean isEmpty(){
        return top == bottom;
    }

    /**
     * 入栈
     * @param llNode 入栈节点
     */
    public void push(LLNode2<T> llNode){
        llNode.next = top;//新节点的next指向顶部
        top = llNode;//top重新指向最顶端
    }

    /**
     * 出栈
     * @return 返回出栈节点
     */
    public LLNode2<T> pop(){
        if (top == bottom){
            throw new RuntimeException("栈为空");
        }
        LLNode2<T> temp;
        temp = top;
        top = top.next;//重新指向上一个节点
        return temp;
    }

    /**
     * 读取栈顶的数据，仅仅读取，不是出栈
     * @return 返回栈顶数据
     */
    public T readLastData(){
        if (top == bottom){
            throw new RuntimeException("栈为空");
        }
        return top.data;
    }

    /**
     * 遍历栈 从顶部开始
     */
    public void list(){
        if(top == bottom){
            System.out.println("栈为空");
            return;
        }
        LLNode2<T> temp = top;
        while (temp!=bottom){
            System.out.print(temp.data + "\t");
            temp = temp.next;
        }
        System.out.println();
    }

    /**
     * 判断是否为运算操作符
     * @param str 符号
     * @return 真假
     */
    public boolean isOperation(Character str){
        return str == '*' || str == '/' || str == '+' || str == '-';
    }

    /**
     * 判断运算符优先级 等级越高，返回数字就大
     * @param str 运算符
     * @return 大小
     */
    public int isPrior(Character str){
        if(str == '*' || str == '/'){
            return 1;
        } else if (str == '+' || str == '-'){
            return 0;
        } else {
            throw new RuntimeException("符号错误");//当输入不是运算操作符时，抛出异常
        }
    }

    public int calculate(Integer num1,Integer num2,Character opera){
        if(opera == '+') return num1+num2;
        if(opera == '-') return num2-num1;
        if(opera == '*') return num1*num2;
        if(opera == '/') return num2/num1;
        throw new RuntimeException("运算错误");
    }
}

6. 波兰表达式

1）前缀表达式

（1) 前缀表达式又称波兰式，前缀表达式的运算符位于操作数之前

（2) 举例说明： (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6

（3）前缀表达式的计算机求值

从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素和次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果

例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下：

从右至左扫描，将6、5、4、3压入堆栈
遇到+运算符，因此弹出3和4（3为栈顶元素，4为次顶元素），计算出3+4的值，得7，再将7入栈
接下来是×运算符，因此弹出7和5，计算出7×5=35，将35入栈
最后是-运算符，计算出35-6的值，即29，由此得出最终结果

2）中缀表达式

（1）中缀表达式就是常见的运算表达式，如(3+4)×5-6

（2）中缀表达式的求值是我们人最熟悉的，但是对计算机来说却不好操作(前面我们讲的案例就能看的这个问题)，因此，在计算结果时，往往会将中缀表达式转成其它表达式来操作(一般转成后缀表达式.)

（3）中缀表达式的计算机求值（如第5节）

3）后缀表达式

（1）后缀表达式又称逆波兰表达式,与前缀表达式相似，只是运算符位于操作数之后

（2）举例说明： (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –

正常的表达式	逆波兰表达式
a+b	a b +
a+(b-c)	a b c - +
a+(b-c)*d	a b c – d * +
a+d*(b-c)	a d b c - * +
a=1+3	a 1 3 + =

（3）后缀表达式的计算机求值

从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素和栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果

例如: (3+4)×5-6 对应的后缀表达式就是 *3 4 + 5 × 6 - *, 针对后缀表达式求值步骤如下

从左至右扫描，将3和4压入堆栈；
遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
将5入栈；
接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
将6入栈；

最后是-运算符，计算出35-6的值，即29，由此得出最终结果

4）中缀表达式转后缀表达式

（1）思路分析

1) 初始化两个栈：运算符栈operaStack和储存中间结果的栈tempStack；
2) 从左至右扫描中缀表达式；
3) 遇到操作数时，将其压tempStack；
4) 遇到运算符时，比较其与operaStack栈顶运算符的优先级：
- 1.如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
- 2.否则，若优先级比栈顶运算符的高，也将运算符压入operaStack；
- 3.否则，将operaStack栈顶的运算符弹出并压入到tempStack中，再次转到4)与operaStack中新的栈顶运算符相比较；注意：有时会遇到与“（”比较优先级，遇到此情况时，直接将运算符压入，也就是说此处认为“（”优先级最低。
5) 遇到括号时：
- (1) 如果是左括号“(”，则直接压入operaStack
- (2) 如果是右括号“)”，则依次弹出operaStack栈顶的运算符，并压入tempStack，直到遇到左括号为止，此时将这一对括号丢弃
6) 重复步骤2至5，直到表达式的最右边
7) 将operaStack中剩余的运算符依次弹出并压入tempStack
8) 依次弹出tempStack中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

这里注意：因为tempStack这个栈后续没有pop操作，并且还需要逆序输出，为了方便此处使用List，后期直接返回list即可。

例子:1 + ( ( 2 + 3 )× 4) - 5

扫描到的元素	tempStack(栈底->栈顶)	operaStack (栈底->栈顶)	说明
1	1	空	数字，直接入栈
+	1	+	s1为空，运算符直接入栈
(	1	+ (	左括号，直接入栈
(	1	+ ( (	同上
2	1 2	+ ( (	数字
+	1 2	+ ( ( +	s1栈顶为左括号，运算符直接入栈
3	1 2 3	+ ( ( +	数字
)	1 2 3 +	+ (	右括号，弹出运算符直至遇到左括号
×	1 2 3 +	+ ( ×	s1栈顶为左括号，运算符直接入栈
4	1 2 3 + 4	+ ( ×	数字
)	1 2 3 + 4 ×	+	右括号，弹出运算符直至遇到左括号
-	1 2 3 + 4 × +	-	-与+优先级相同，因此弹出+，再压入-
5	1 2 3 + 4 × + 5	-	数字
到达最右端	1 2 3 + 4 × + 5 -	空	s1中剩余的运算符

5）Java程序实现

package datastructure;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

/**
 * 加入中缀表达式转后缀表达式后计算
 * Created by qjq on 2020/1/31 10:09
 */
public class PolandNotationPro {
    public static void main(String[] args) {
        //String mediumExpression = "(3+4)*5-6";//"3 4 + 5 * 6 -"
        String mediumExpression = "1+((2+3)*4)-5";//[1,2,3,+,4,*,+,5,–]
        List<String> suffixExpression;
        List<String> expression = toArrayList(mediumExpression);
        System.out.println("mediumExpression="+expression);
        suffixExpression = toSuffixExpression(mediumExpression);
        System.out.println("suffixExpression="+suffixExpression);
        int result = calculate(suffixExpression);
        System.out.println("结果为："+result);

    }

    /**
     * 将任意格式字符串转换为list，方便遍历
     * @param suffixExpression 逆波兰表达式
     * @return 返回ArrayList
     */
    public static List<String> toArrayList(String suffixExpression){
        List<String> expression = new ArrayList<>();
        char c;//用于遍历suffixExpression
        String str;//用于拼接字符
        int i=0;
        while (i < suffixExpression.length()){
            c = suffixExpression.charAt(i);
            //0的ASCII码对应48，9的ASCII码对应57,空格的ASCII码32，回车13
            //换行10
            if (c == 32||c == 13||c == 10){
                //如果是空格、回车、换行不做处理，略过
                i++;
            }else if (c < 48 || c > 57) {//当不是数字时
                expression.add(""+c);//直接放入list中
                i++;
            }else{//当为一个数时，需要考虑多位数
                str = "";
                while (i < suffixExpression.length() && (c=suffixExpression.charAt(i)) >= 48 && (c=suffixExpression.charAt(i)) <= 57) {
                    str += c;//拼接
                    i++;
                }
                expression.add(str);
            }
        }
        return expression;
    }

    /**
     * 计算后缀表达式
     * @param expression 后缀表达式
     * @return 计算结果
     */
    public static int calculate(List<String> expression){
        Stack<String> stack = new Stack<>();
        for (String ele :
                expression) {
            //遇到数字时，将数字压入堆栈
            if(ele.matches("\\d+")){//匹配多位数
                stack.push(ele);
            }else {
                //遇到运算符时，弹出栈顶的两个数，
                // 用运算符对它们做相应的计算（次顶元素 和 栈顶元素），
                // 并将结果入栈
                Integer num1 = Integer.parseInt(stack.pop());
                Integer num2 = Integer.parseInt(stack.pop());
                int cal = singleCal(num1, num2, ele);
                stack.push(Integer.toString(cal));
            }

        }
        return Integer.parseInt(stack.pop());
    }

    /**
     * 加减乘除的计算
     * @param num1 数1
     * @param num2 数2
     * @param opera 运算符
     * @return 结果
     */
    public static int singleCal(Integer num1,Integer num2,String opera){
        if(opera.equals("+")) return num1+num2;
        if(opera.equals("-")) return num2-num1;
        if(opera.equals("*")) return num1*num2;
        if(opera.equals("/")) return num2/num1;
        throw new RuntimeException("运算错误");
    }

    public static List<String> toSuffixExpression(String mediumExpression){
        List<String> mediumExp = toArrayList(mediumExpression);
        Stack<String> operaStack = new Stack<>();//运算符栈
        //说明:因为tempStack这个栈后续没有pop操作，并且还需要逆序输出，为了方便此处使用List
        //Stack<String> tempStack = new Stack<>();//储存中间结果栈
        List<String> tempList = new ArrayList<>();

        for (String ele :
                mediumExp) {
            //遇到数字时，将数字压入tempList
            if(ele.matches("\\d+")){//匹配多位数
                tempList.add(ele);
            }else {//4) 遇到运算符时，比较其与operaStack栈顶运算符的优先级：
                //1.如果operaStack为空，或运算符为左括号“(”，则直接将此运算符入栈；
                if(operaStack.isEmpty()||ele.equals("(")){
                    operaStack.push(ele);
                }else if (ele.equals(")")){
                    //如果是右括号“)”，则依次弹出operaStack栈顶的运算符，
                    // 并压入tempList，直到遇到左括号为止，此时将这一对括号丢弃
                    String str;
                    while(!(str = operaStack.pop()).equals("(")){
                        tempList.add(str);
                    }
                }else {//2.为+-/*时，若优先级比栈顶运算符的高，也将运算符压入operaStack；
                    //当前优先级小于等于栈顶运算符时
                    while(operaStack.size()!=0 && isPrior(ele)<=isPrior(operaStack.peek())){
                        tempList.add(operaStack.pop());
                    }
                    //还需要ele压入operaStack
                    operaStack.push(ele);
                }

            }

        }
        //将operaStack中剩余的运算符依次弹出并压入tempList
        while(!operaStack.isEmpty()){
            tempList.add(operaStack.pop());
        }
        return tempList;
    }
    /**
     * 判断运算符优先级 等级越高，返回数字就大
     * 注意： “（”不算运算操作符，返回-1
     * @param str 运算符
     * @return 大小
     */
    public static int isPrior(String str){
        switch (str) {
            case "*":
            case "/":
                return 1;
            case "+":
            case "-":
                return 0;
            case "(":
                return -1;
            default:
                throw new RuntimeException("符号错误");//当输入不是运算操作符时，抛出异常

        }
    }

}